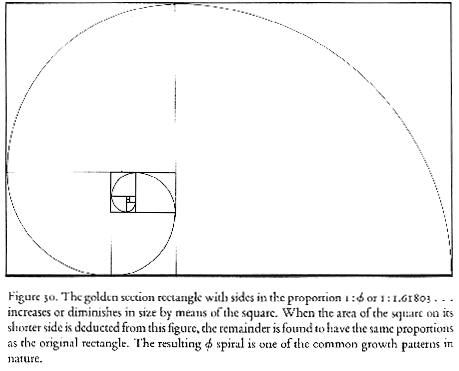
Rectangles formed from the golden section creating the spiral pattern found in nature
If you have a rectangle whose sides are related by phi (say, for instance, 13 x 8), that rectangle is said to be a Golden Rectangle.
If you divide the above rectangle's long side according to the Golden Mean you will produce the square that you see on the right of the rectangle. If you then divide the central line inside the rectangle according to the Golden Mean you will create another square in the top left hand corner of the rectangle.
If you continue dividing the next line inside the rectangle you create a smaller square in the bottom left hand corner of the rectangle. If you continue this dividing and then draw a line through all the points that you have divided you will end up with a spiral pattern (see above).
This pattern, created by the Golden Mean is found in snail shells, spiral nebulae of galaxies and the petal arrangement of daisies and roses. The Golden Mean proportions were used in the construction of the Greek Parthenon and the Egyptian Pyramids. Since the Renaissance, the Golden Mean has been used extensively in art and architecture, it figures for example in the Venetian Church of St. Mark built early in the 16th century.
It has become a standard proportion for width in relation to height as used in facades of buildings, in window sizing, in first story to second story proportion, and in the dimensions of paintings and picture frames.
The Fibonacci series relates to all of the musical intervals, which comprise beautiful chords. The following table shows some Fibonacci ratio musical chords using the fundamental tone A:
| A |
A |
D |
F |
E |
C |
E |
C# |
F# |
C# |
D |
F |
| root |
octave |
4th |
aug.5th |
5th |
min3rd |
5th |
3rd |
6th |
3rd |
4th |
aug.4th |
| 1/1 |
2/1 |
2/3 |
2/5 |
3/2 |
3/5 |
3/8 |
5/2 |
5/3 |
5/8 |
8/3 |
8/5 |
The Fibonacci ratios were also utilised in sacred temple architecture, including the towering Gothic Cathedrals. Guillaume Dufay (c. 1400-1474) from the Netherlands composed music for the dedication of Florences cathedral of Santa Maria del Fiore in 1436.
His musical piece was based on the Fibonacci series of tones, which corresponded to the dimensions of the cathedrals dome. These musical temples were part of the medieval renaissance of sacred geometry, Hermetic mysteries and the flowering of art and music.
The French architect LeCorbusier noted that the human body when measured from foot to navel and then again from navel to top of head, showed average numbers very near to the Golden Ratio. He extended this to height compared with arm-span, and designed doorways consonant with these numbers.
Studies have shown that the patterns of tree branching adhere to the Golden Mean proportion, although again not exactly, while the dendritic cracking in certain metallic alloys which occurs at very low temperatures is Golden Mean based.
Mike Kay found that many of Mozart's sonatas divide into two parts exactly at the Golden Section point. Was this a conscious choice or did he do this intuitively? His sister said he was always playing with numbers and was fascinated by mathematics (American Scientist March/April 1996).
DIVINE PROPORTIONS AND THE GOLDEN MEAN
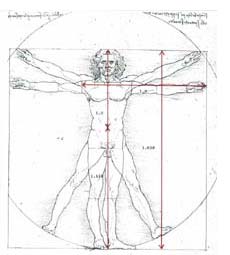
If the top of head to belly button = 1
then belly button to bottom of the feet = 1.618
If the shoulder to fingertip = 1
then the ideal height of man or woman = 1.618

Each succeeding finger bone is 1.618 the length of the preceding finger bone.
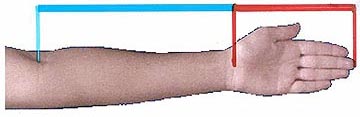
The distance from elbow to wrist is 1.618 the distance from wrist to fingertip.
All beautiful faces regardless of race, age, sex, and other variables conform to the Divine Proportion.
Reproduced from - www.facialbeauty.org/divineproportion.html